Avklare behov og forberede konkurransen

Kva er ein relativ poengmodell?

Dei relative poengmodellane er kjenneteikna ved at pris/kostnad og dei kvalitative kriteria blir vurderte i relasjon til kvarandre og ikkje opp mot førehandsfastsette kriterium. Både pris/kostnad og dei kvalitative kriteria blir vurderte ut frå ein poengskala der også omsynet til vektinga mellom kriteria blir varetatt.

Dei relative poengmodellane finst i ei rekke variantar. Dei mest vanlege variantane er poengmodellane der ein tar utgangspunkt i at lågaste pristilbod gir maksimal poengscore og der poenga for dei andre pristilboda blir vurderte opp mot lågaste pristilbod. Dei mest brukte modellane i denne kategorien er lineær og forholdsmessig metode.

Ei utfordring med å rekne om pris til poeng samtidig med at ein gir dei kvalitative kriteria poeng og vurderer desse samla innanfor eit felles poengsystem, er at ein då samanliknar «eple og pærer» (pris og kvalitet).

For dei relative poengmodellane der lågaste pris/kostnad blir gitt maksimalt poeng (dei modellane som er mest brukte), er det også ei utfordring knytt til samanlikninga med dei kvalitative kriteria. Dei kvalitative kriteria vil ofte bli vurderte opp mot nokre vurderingstema, og det er ein risiko for at ingen av tilboda blir gitt maksimumspoeng ut frå desse kriteria.

Det blir derfor anbefalt at du gjer ei justering av poenga for dei kvalitative krava ("normalisering") slik at poengskalaen blir utnytta på same måte som for pris- eller kostnadsskalaen. På denne måten helde de fast ved opphavleg vekting mellom pris/kostnad og dei kvalitative kriteria. 

Vidare er det slik at når poeng blir rekna ut for pris eller kostnad og kvalitet, er dei relative modellane konstruerte slik at det vil vere ein risiko for at det tilbodet som f.eks. endar opp med høgaste (beste) poengscore for både pris og kvalitetselementa, kan påverkast av eit irrelevant tilbod med lågaste pris, men dårleg kvalitet. Sagt med andre ord så vil prisnivået på tilbodet med lågast pris kunne påverke kven av dei andre tilboda med høgare kvalitet som vinn konkurransen.

Felles utfordring for dei relative prismodellane er at dei også gjer det tydeleg kor viktig det er at du som oppdragsgivar har høve til å redusere risiko for feil val ved å utføre modellsimuleringar for på den måten å avdekke moglege uheldige utslag av modellen før tildeling av kontrakt.

Vi har nedanfor beskrive ein del relative poengmodellar, men finn det vanskeleg å anbefale ein enkelt modell. Modellane har alle sine sterke og svake sider og nokre kan også i enkelte tilfelle vere ulovlege å bruke.

Under følger nokre poengmodellar relaterte til lågaste pris.

Lineær modell

Basismodell: Basis lineær modell inneber at forskjellar i poengscore speglar prosentforskjellen i pris (frå lågaste tilbod). Formelen kan beskrivast slik:

Ei generell utfordring med bruk av den lineære metoden er at tilbod som er meir enn dobbelt så dyre som billigaste tilbod, oppnår minuspoeng, som i realiteten inneber å auke poengspennet og dermed oppnår tildelingskriteriet større vekt enn tilsikta. Dersom modellen gir negative poeng for vurdering av pris men ikkje for andre kriterium, vil dette i utgangspunktet vere ulovleg, jf. KOFA-sak 2007/131.Dersom du opplyser om at det er mogleg i konkurransegrunnlaget, kan det likevel vere tillate, jf KOFA 2015/60.

Eit råd kan vere å utvide den lineære modellen slik at dyraste pristilbod får 0 poeng sjølv om det er meir enn dobbelt så dyrt. I KOFA-sak 2011/203 blei ein lineær metode godtatt der dyraste tilbod som fekk 0 poeng, var 150 % dyrare enn billigaste tilbod. Føresetnaden for å gjere dette må vere at poengskalaen er tilstrekkeleg vid til at det er mogleg å premiere dei relevante forskjellane mellom tilboda.

Lineær modell med fast prosentsats

Ein variant av den lineære basismodellen er publisert av den danske Konkurransestyrelsen. Her gir framleis billigaste pristilbod maksimalpoeng mens lågaste pris pluss ein fastsett prosent gir minimumspoeng. Alternativt kan ein også operere med ein pris som er det maksimale av det ein ønsker å betale og som då gir minimumspoeng.

Modellen er enkel å bruke og enkel å forklare, men det kan vere ei utfordring å fastsette prosentsatsen X som skal utløyse minimumspoeng slik at modellen er eigna til å spegle dei forventa spreiingane i tilbodsprisane. Føreset god kjennskap til marknadsprisane.

Variant 1: Intervallmodell

Modellen inneber at oppdragsgivar set opp ei matrise, der lågaste pris får maks poeng, og høgaste pris minst poeng, og dei andre tilboda graderte etter gitt prisspenn. Matrisa må settast opp etter at tilboda er opna, slik at ein veit at spennet på intervalla og ytterpunkta passar for tilfellet. Formelen for modellen er:

Storleik på intervallet (i kroner)=(Høgaste pris-lågaste pris) / talet på intervall 

Døme: Høgaste pris er kr 17 000, lågaste pris er 10 000, talet på intervall blir sett til 10. Poenggivinga blir då som følger:

Forholdsmessig modell

Forholdsmessig modell inneber at differansen i poeng blir mindre jo høgare prisforskjellane er frå lågaste pris. Formel for forholdsmessig modell:

Den forholdsmessige metoden inneber at fråtrekk i poeng svarer til den relative pris- og kvalitetsforskjellen. Sagt på ein annan måte: Poengforskjellen blir mindre, jo høgare prisforskjellen er. Dette kan resultere i uventa avvikande poengscorar når det kjem til forskjell i pris. I metoden vil nivået på den lågaste tilbodsprisen vere styrande for utteljinga på dei andre tilbodsprisane. Metoden fører vidare til større poengutslag i intervallet nært opp til den lågaste prisen, og små poengutslag ved høgare tilbodsprisar.

Ingen tilbod vil kunne få poengscore 0 eller minuspoeng i denne modellen.

KOFA har i fleire saker vurdert om den forholdsmessige modellen er ulovleg å bruke, jf særleg KOFA-sak 2014/95. Til no har KOFA kome til at den forholdsmessige metoden ikkje i seg sjølv er ulovleg å nytte i evalueringa, men det er viktig at han berre blir nytta i tilfelle der han er eigna til å påvise relevante forskjellar mellom tilboda.

Hybridmodell

I den såkalla Hybridmodellen (utvikla av Oslo kommune) er den matematiske formelen som er brukt, laga slik at han er lineær inntil eit gitt knekkpunkt, då han går over til å bli forholdsmessig. 

Hybridmodellen tar delvis høgde for problemet med strategisk prising, samtidig som han bruker skalaen i større grad enn ein rein forholdsmessig metode vil gjere. Hybridmodellen er matematisk meir komplisert.

Poengfrådragsmodellane

Poengfrådragsmodellen inneber at billigaste tilbod får maksimal poengscore, og dei andre tilboda får frådrag i poeng etter kor mykje dei skil seg frå dette tilbodet, etter ein faktor ein set sjølv.

Modellen finst i to variantar, ein prosentvariant og ein prisvariant.

I prosentvarianten avgjer ein kor mange prosent dyrare (X) eit tilbod må vere for å få eitt poeng frådrag, mao. kor dyrt eitt poeng er.  Formel prosentmetode:

Ved prisvarianten avgjer ein kor mange kroner dyrare (X) eit tilbod må vere for å få eitt poeng frådrag, mao. kor dyrt eitt poeng er. Formel kronemetode:

Poengmodell der gjennomsnittsprisen i tilboda er utgangspunkt for poengutrekning

Gjennomsnittsmodell - matrise

Gjennomsnittsmodell med matrise baserer seg på at vurdert pris får poeng relativt til gjennomsnittspris på alle innleverte tilbod etter ei oppstilt matrise. Gjennomsnittspris blir fiksert mot gjennomsnittspoengsum. Tilboda blir så sette i ei matrise ut i frå gjennomsnittsprisen, med ein korresponderande poengsum.

Eksempel: Poengspennet er frå 1 til 5, så gjennomsnittspoengsum er 3. Første intervall er sett til 5 %, som gir eitt poeng frådrag eller tillegg viss eit tilbod er meir enn 5 % høvesvis dyrare eller billigare enn gjennomsnittsprisen. Neste intervall er sett til 25 % og gir 2 poeng frådrag/tillegg. Eksemplet kan beskrivast i følgande figur: 

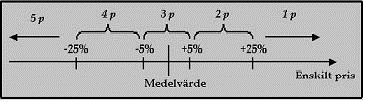
Modellen er ytterlegare beskriven i artikkelen "Metoder vid utvärdering av pris och kvalitet i offentlig upphandling".

Relative poengmodellar knytte til referansepris

I staden for å vurdere det enkelte tilbodet mot ein referansepris som baserer seg på eitt eller fleire av dei andre tilboda, kan ein fiksere referanseprisen. Ein set då ein fiktiv, ønskt prisstorleik, og måler tilboda opp mot denne. Referanseprisen kan for eksempel vere høgaste pris ein er villig til å betale, budsjettert pris eller ein berekna pris.

Ein generell fordel med å nytte fikserte referanseprisar er at ein kan unngå problemet med at poenggivinga blir påverka av dei andre tilboda. Dermed vil ein ikkje oppleve dei same ulempene som i eksempla over, der vinnande tilbod varierte med den lågaste prisen (frå eit irrelevant tilbod). Ein unngår samtidig at leverandørane kan manipulere evalueringsmodellen.

Truleg kan dei fleste andre modellar for poengsetting av pris også brukast med fikserte referanseprisar, der ein for eksempel byter ut lågaste pris med ein fiksert referansepris. Her gir vi 2 eksempel på modellar knytte til referansepris.

1.  Referansepris – høgaste akseptable pris

Ved denne modellen for fiksert referansepris set ein som fiksert referansepris det som er høgaste akseptable pris å betale. Tilbodet med lågaste pris får topp score. Andre tilbod får poeng etter dette, basert både på denne referansepris og lågaste pris. Slik sett varetar ikkje denne metoden ein av fordelane med referansepris, fordi lågaste pris påverkar vurderinga av kvart tilbod. Modellen er også kalla Targetpris. Modellen kan beskrivast med følgande formel:

Ei ulempe med denne modellen er at han blir påverka av lågaste pris.

2.  Middels poeng med målpris

I ein evalueringsmetode publisert av den danske Konkurransestyrelsen bruker dei ein målpris som utgangspunkt. Denne målprisen tilsvarer ein middels poengverdi. Dei andre prisane gir poeng ut frå målprisen etter ein lineær berekningmetode. Minimums- og maksimumspoeng blir fastsett til pluss minus X % i forhold til målpris.

Fordelar: Same fordelar som modellen over.

Ulemper: Vanskeleg å fastsette ein målpris som er midt i spennet av tilbodsprisane – krev god marknadskunnskap.

Modellen har ei utfordring når det gjeld å fastsette prosentsatsen som skal utløyse maksimums- og minimumspoeng.

Modellen eignar seg best dersom målprisen ikkje blir offentleggjord og ein har høve til å justere denne ut frå dei tilbydde prisane.